Сравнение систем
СС могут быть с произвольной основой, но популярны 2,8,10,16-ые.
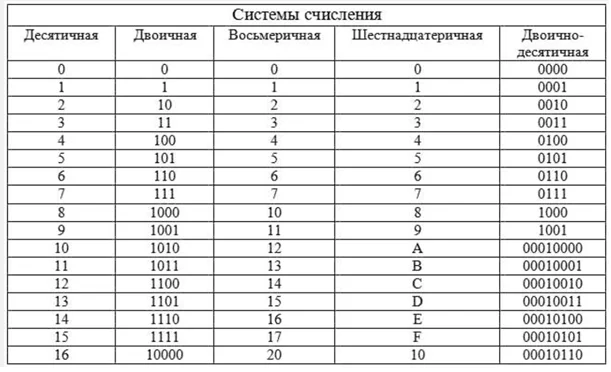
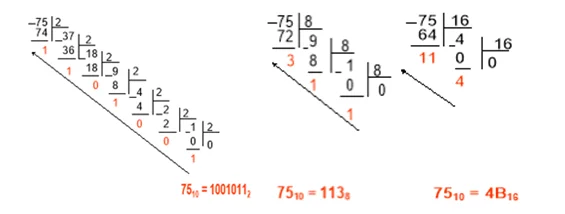
Правила перевода из двоичной, восьмеричной и шестнадцатеричной в 10СС:
Исходный вариант следует разделить на тройки цифр, с крайней справа. Если не хватает, старший разряд дополнить 0. Далее под каждой триадой ставится подходящий символ из 8‑ой системы.
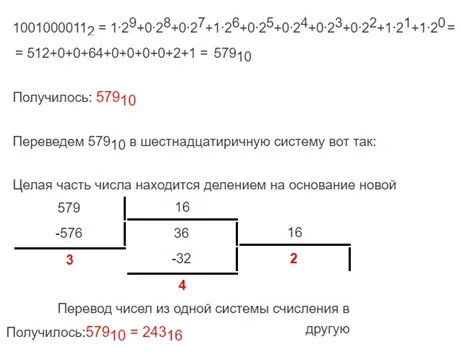
Рассмотрим перевод на примере числа 579, которое соответствует 10010000112
001 001 000 011
Правила перевода из двоичной в шестнадцатеричную систему счисления:
Число разбивается по 4 знака, начиная справа (с меньшего разряда). Если не будет хватать символов у старшего разряда, тетраду дополняют нулями.
10010000112
0010 0100 0011
Сравнительный перевод дробей в СС
Чтобы перевести правильные дроби из 10-ой СС в другие позиционные, следует придерживаться правила, которое хорошо видно на примере перевода числа 0,35:
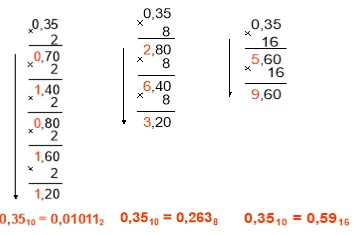
Удобно писать над каждой цифрой порядок, а дальше ее умножить на основу СС в степени разряда.
Часть 3:
Урок 1:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 2:
1
2
3
4
5
6
7
8
9
10
Урок 3:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 4:
1
2
3
4
5
6
7
8
9
10
11
Урок 5:
1
2
3
4
5
6
7
8
9
10
Урок 6:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 7:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 8:
1
2
3
4
5
6
7
8
9
10
Урок 9:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 10:
1
2
3
4
5
6
7
8
9
10
11
Урок 11:
1
2
3
4
5
6
7
8
9
10
Урок 12:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 13:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 14:
1
2
3
4
5
6
7
8
9
10
Урок 15:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 16:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 17:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 18:
1
2
3
4
5
6
7
8
9
Урок 19:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 20:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 21:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 22:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 23:
1
2
3
4
5
6
7
8
Урок 24:
1
2
3
4
5
6
7
8
9
Урок 25:
1
2
3
4
5
6
7
8
9
10
Урок 26:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 27:
1
2
3
4
5
6
7
8
Урок 28:
1
2
3
4
5
6
7
8
9
10
11
Урок 29:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 30:
1
2
3
4
5
6
7
8
9
10
11
Урок 31:
1
2
3
4
5
6
7
8
9
10
Урок 32:
1
2
3
4
5
6
7
8
9
Урок 33:
1
2
3
4
5
6
7
8
9
10
11
Урок 34:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 35:
1
2
3
4
5
6
7
8
9
Урок 36:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 37:
1
2
3
4
5
6
7
8
9
10
Урок 38:
1
2
3
4
5
6
7
8
Урок 39:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 40:
1
2
3
4
5
6
7
8
9
10
11
Повторение:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Непозиционные СС, их особенности
Первоначально древние люди ставили отметки (черточки-зарубки, точки), чтобы обозначить количество того или иного предмета. Отклики этого подхода все еще встречаются (полоски у военных, счетные палочки).
Постепенно от единиц они переходили к группам предметов по 3, 5, 10 единиц. Постепенно такие группы стали обозначаться определенными символами, что позволило сократить размер записи.
Римская СС
В ней определенным цифрам отвечают латинские буквы. Их сумма и будет числом.
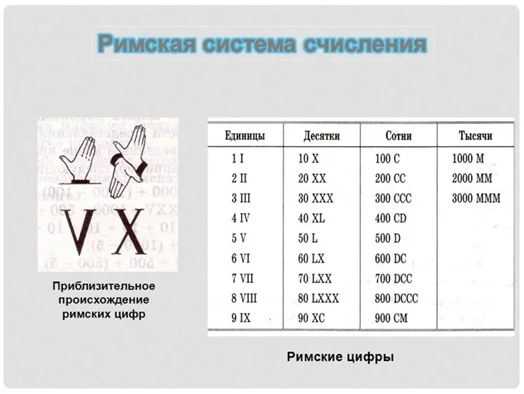
Основные рекомендации при пользовании римскими цифрами:
- Символы следует писать по убыванию слева направо.
- Нежелательно записывать подряд более 3 одинаковых знаков.
- Положение цифры обозначает, какой ее вклад – отрицательный, если она стоит слева от большего числа, положительный – справа.
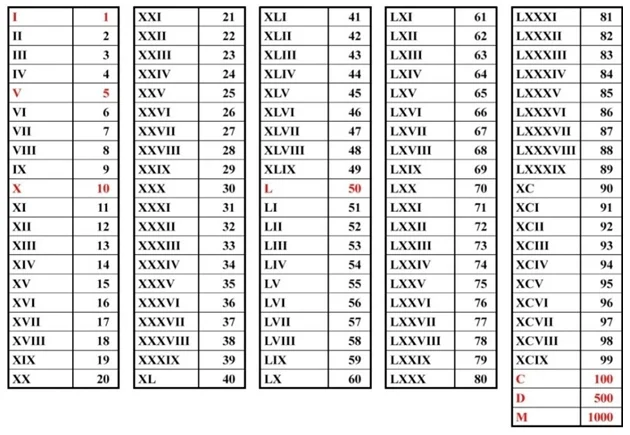Таблица римских цифр
Недостаток этой СС в том, что для больших чисел недоступны операции сложения или другие, ещё она сложная и громоздкая. Зато римские цифры отлично вписались там, где нужна нумерация и эстетика: циферблаты, номера глав, списки, серии документов.
Основные позиционные СС, правила перевода
Двоичная система счисления
Систему, на которой основывается работа компьютеров, придумал гениальный немецкий ученый Г.В. Лейбниц (еще до 19 века!). Он придумал и описал СС, в которой все вычисления проводятся при помощи двух простейших символов – 0 и 1.
Компьютер, как механическое устройство, получает команды в виде двоичной кодировки. Он не в силах понять сложные задания, человеческую речь, музыку или тысячи оттенков, а переводя/кодируя всю необходимую информацию при помощи 0 и 1 (сеть, отсутствие сети), можно передать ему любые команды или информацию. Естественно, такие задания выглядят как огромные массивы двух знаков.
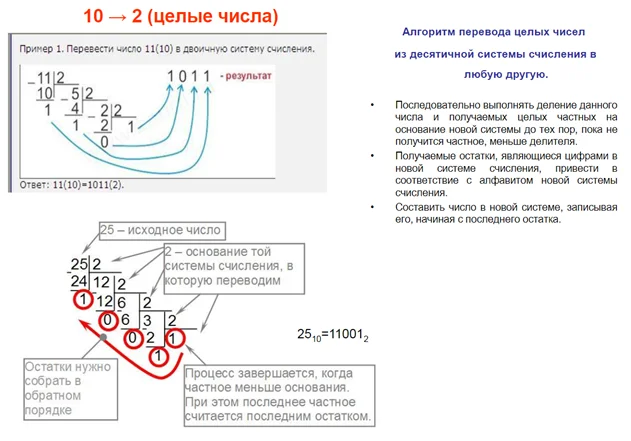
Алгоритм перевода чисел из десятичной в двоичную систему:
- Деление на основу СС до тех пор, пока не останется в остатке значение меньше значения основы.
- Записать остатки, от последнего к первому.
- Первый ноль можно не писать.
111 0100 11002
Этот порядок действия позволят переводить в любую позиционную СС. В данном случае, основа – 2, остаток < или равен =.
Обратный алгоритм перевода из двоичной в десятичную систему счисления:
Записать число развернуто, то есть, сколько сотен, десятков и единиц в нем, но учитывая основу – 2
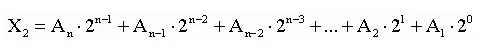
Объяснение. Развернутая форма записи 579: 5*102+7*101+9*10= 57910.
Обычно мы пользуемся свернутой формой записи чисел, то есть без разбивки на разряды и умножения на основу.
- Умножить и суммировать полученные значения.
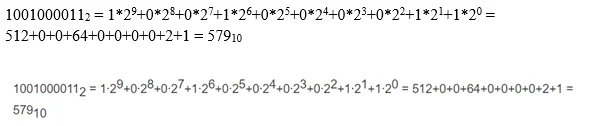
А чтобы было легче, пользуются готовой таблицей степеней 2.
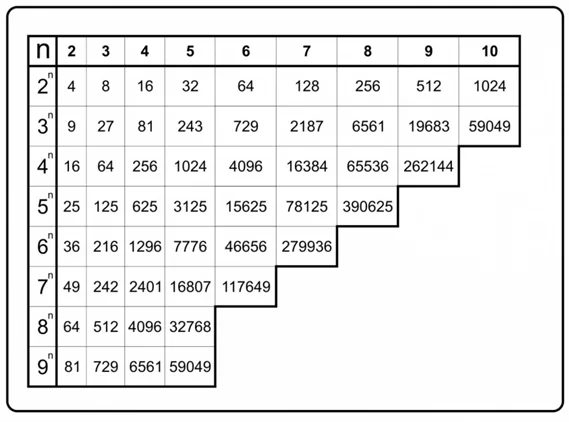
Альтернативный способ преобразования для гуманитариев
Для начала нужно написать степени двойки, начиная с самой большой:
Далее нужно отнимать от числа максимальную степень двойки и напротив нее ставить 1, если есть в исходном варианте или 0, если его нет. Перевод числа 579
Обратно еще проще. Подсчитать количество знаков – это будет степень 2 в степени -1. И так далее. А проще при помощи той же таблицы:
Если же оно на 1 больше, то число будет начинаться и заканчиваться на 1, а внутри – сплошные 0.
Восьмеричная СС
Основой такой системы является 8, а числа восьмеричной системы 0-7. Данная система счисления является позиционной и целочисленной. Применяется в сферах, связанных с цифровыми технологиями, особенно в Linux-программном обеспечении (права доступа, исполнения).
Пример: Перевести 5798 из десятичной в восьмеричную систему счисления:
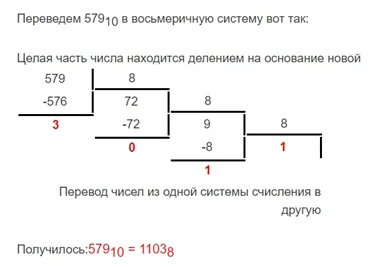
Обратный перевод из восьмеричной СС в десятичную:
11038 = 1∙83+1∙82+0∙81+3∙8 = 512+64+0+3 = 57910
Таблица степеней
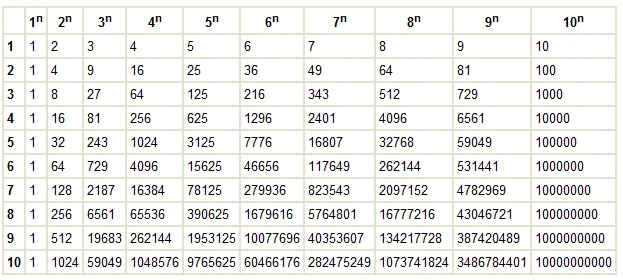
Альтернативный вариант таблицы степеней
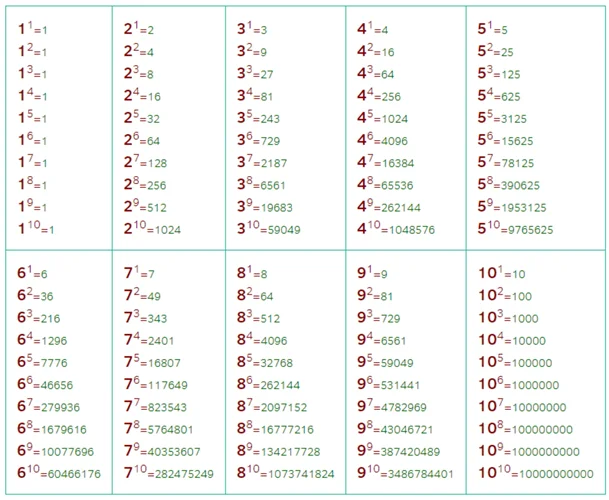
Системы счисления – виды, особенности
Система счисления (СС) – способ выражения чисел при помощи специальных правил и знаков, которые называются цифрами.
Все существующие системы делят на 2 группы:
- Позиционные системы счисления – такие, в которых, в зависимости от положения, цифры будет иметь разное значение. К этой группе относится арабская СС, в которой на первом месте справа цифра будет обозначать единицы, на втором – десятки, на третьем – сотни и так далее.
Чтобы выразить число 475, достаточно по порядку написать 3 символа, 475, выражая 5 единиц, 7 десятков и 4 сотни.
К этой группе также относятся СС с различными основаниями (2,8,16).
- Непозиционные СС – имеет значение именно знак, а не его положение. Единицы, десятки, сотни обозначаются определенными символами. Яркий представитель этой группы – римская СС.
Еще одна особенность – чтобы выразить число и не использовать сотни символов, применяется прибавление и вычитание. Написать 475 римскими знаками можно так CCCCXXXXXXXIIIII, но это нерационально. Если отнимать или прибавлять цифры, получится меньшее количество символов – CDLXXV. Цифра слева означает, что ее нужно отнять от большего числа, а справа – прибавить.
12 – XII
8 – VIII или IIX
Правильным считается тот вариант, при котором получается меньше символов.
Интересно. Первой позиционной СС была вавилонская и была она шестнадцатиричная! А в 19 веке использовали двенадцатеричную СС.
Алфавит СС – знаки, которые используются для обозначения цифр.
Основание – количество знаков, которыми кодируются числа. Еще оно показывает отличие между цифрами на разных позициях. Основание – целое число, начиная с 2.
Важно. Если в тексте идет речь о различных системах, то чтобы уточнить, какая используется основа, ставится подстрочный знак: 12548, 011001112
Примеры? Если же обозначения нет, по умолчанию это десятичная (12549).
Разряд – положение, позиция обозначения цифры в числе. Пример?
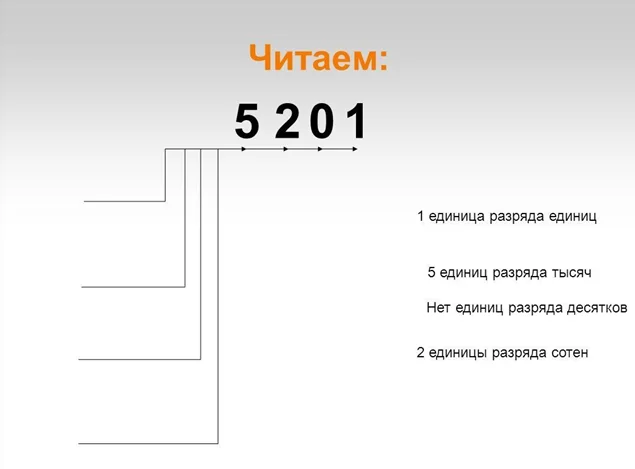
Часть 1:
Урок 1:
1
2
3
4
5
6
7
8
Урок 2:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 3:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 4:
1
2
3
4
5
6
7
8
9
Урок 5:
1
2
3
4
5
6
7
8
9
10
Урок 6:
1
2
3
4
5
6
7
8
9
10
11
Урок 7:
1
2
3
4
5
6
7
8
9
10
Урок 8:
1
2
3
4
5
6
7
8
9
10
Урок 9:
1
2
3
4
5
6
7
8
9
10
11
Урок 10:
1
2
3
4
5
6
7
8
9
Урок 11:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 12:
1
2
3
4
5
6
7
8
9
10
Урок 13:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 14:
1
2
3
4
5
6
7
8
9
Урок 15:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 16:
1
2
3
4
5
6
7
8
9
Урок 17:
1
2
3
4
5
6
7
8
9
Урок 18:
1
2
3
4
5
6
7
8
9
10
Урок 19:
1
2
3
4
5
6
7
8
9
10
Урок 20:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 21:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 22:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 23:
1
2
3
4
5
6
7
8
9
10
Урок 24:
1
2
3
4
5
6
7
8
9
10
11
Урок 25:
1
2
3
4
5
6
7
8
9
Урок 26:
1
2
3
4
5
6
7
8
9
10
Урок 27:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 28:
1
2
3
4
5
6
7
8
9
10
11
Урок 29:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 30:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 31:
1
2
3
4
5
6
7
8
9
10
Урок 32:
1
2
3
4
5
6
7
8
9
Урок 33:
1
2
3
4
5
6
7
8
9
10
Урок 34:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 35:
1
2
3
4
5
6
7
8
9
10
Урок 36:
1
2
3
4
5
6
7
8
9
10
Урок 37:
1
2
3
4
5
6
7
Урок 38:
1
2
3
4
5
6
7
8
9
10
11
Урок 39:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 40:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Дополнительные задачи:
1
2
3
4
5
6
7
Таблицы истинности
При помощи тех же нулей и единиц создаются таблицы истинности логических выражений, в которых описаны всевозможные варианты.
Основные логические операции
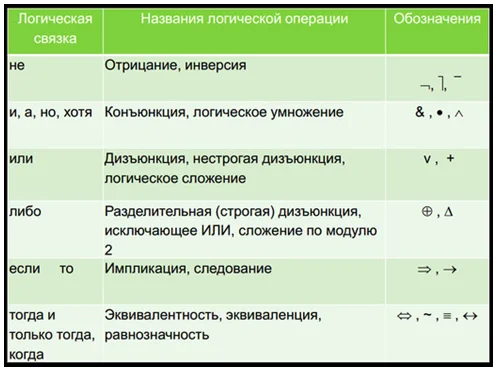
Например, конъюнкция является одной из логических операций. Она является истиной только в том случае, если два высказывания имеют истинные значения.
Логические переменные таблицы истинности обозначают p и q, а их значения выражают при помощи 0 и 1, где 0 – ложь, 1 – истина:
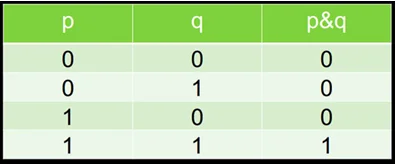
Фрагмент таблицы истинности для конъюнкции.
Так выражаются условия для всех логических операций.
Применяются таблицы истинности еще с начала 20 века в алгебре, логике, программировании.
Разряды чисел
Каждая цифра в записи многозначного числа занимает определённое место — позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.
Разряд числа — это позиция (место) цифры в записи числа.
Счёт разрядов идёт справа налево. То есть, первая цифра справа в записи числа называется цифрой первого разряда, вторая цифра справа — цифрой второго разряда и т. д. Например, в первом классе числа 148 951 784 296, цифра 6 является цифрой первого разряда, 9 — цифра второго разряда, 2 — цифра третьего разряда:
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:
- Единицы называют единицами первого разряда (или простыми единицами) и пишутся на первом месте справа.
- Десятки — единицами второго разряда и пишутся в числе на втором месте справа.
- Сотни — единицами третьего разряда и пишутся на третьем месте справа.
- Единицы тысяч — единицами четвёртого разряда и пишутся на четвёртом месте справа.
- Десятки тысяч — единицами пятого разряда и пишутся на пятом месте справа.
- Сотни тысяч — единицами шестого разряда и пишутся в числе на шестом месте справа и так далее.
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Пример. Запишите цифрами число, которое содержит:
1) 37 единиц второго класса и 565 единиц первого класса;
2) 450 единиц второго класса и 9 единиц первого класса;
3) 8 единиц второго класса и 50 единиц первого класса.
Решение:
1) 37 565;
2) 450 009;
3) 8 050.
Все разрядные единицы, кроме простых единиц, называются составными единицами. Так, десяток, сотня, тысяча и т. д. — составные единицы. Каждые 10 единиц любого разряда составляют одну единицу следующего (более высокого) разряда:
| 10 единиц | = | 1 десяток; |
| 10 десятков | = | 1 сотня; |
| 10 сотен | = | 1 тысяча; |
| 10 тысяч | = | 1 десяток тысяч; |
| 10 десятков тысяч | = | 1 сотня тысяч; |
| 10 сотен тысяч | = | 1 тысяча тысяч (1 миллион); |
и так далее.
Любая составная единица по сравнению с другой единицей, меньшей её называется единицей высшего разряда, а по сравнению с единицей, большей её, называется единицей низшего разряда. Например, сотня является единицей высшего разряда относительно десятка и единицей низшего разряда относительно тысячи.
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, надо отбросить все цифры, означающие единицы низших разрядов и прочитать число, выражаемое оставшимися цифрами.
Например, требуется узнать, сколько всего сотен содержится в числе 6284, т. е. сколько сотен заключается в тысячах и в сотнях данного числа вместе.
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит в числе есть две простые сотни. Следующая влево цифра — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60. Всего, таким образом, в данном числе содержится 62 сотни.
Цифра в каком-нибудь разряде означает отсутствие единиц в данном разряде.
Например, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
24 527 — двадцать четыре тысячи пятьсот двадцать семь.
20 507 — двадцать тысяч пятьсот семь.
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса:
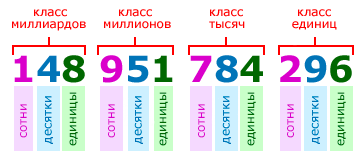
Названия классов многозначных чисел справа налево:
- первый — класс единиц,
- второй — класс тысяч,
- третий — класс миллионов,
- четвёртый — класс миллиардов,
- пятый — класс триллионов,
- шестой — класс квадриллионов,
- седьмой — класс квинтиллионов,
- восьмой — класс секстиллионов.
Для удобства чтения записи многозначного числа, между классами оставляется небольшой пробел. Например, чтобы прочитать число 148951784296, выделим в нём классы:
148 951 784 296
и прочитаем число единиц каждого класса слева направо:
148 миллиардов 951 миллион 784 тысячи 296.
При чтении класса единиц в конце обычно не добавляют слово единиц
.
Шестнадцатеричная СС
Это целочисленная система с основанием 16 (символы шестнадцатеричной системы счисления 0-9 и буквы A – F). Используется в реализации компьютерного программирования и документации на низком уровне, так как 8-битный байт, для записи которого удобно использовать 2 цифры из шестнадцатеричной системы.
Стандарт Юникод использует 4 и более символов 16-ой СС.
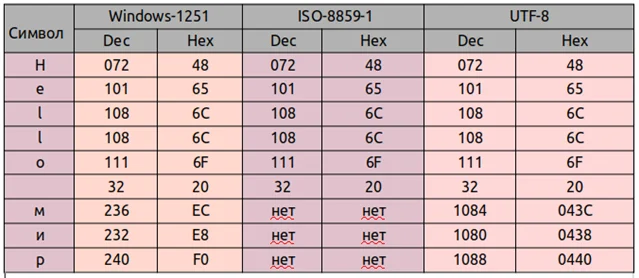
Для записи цвета из красного, зеленого и синего (R, G и B) также используют эту систему.
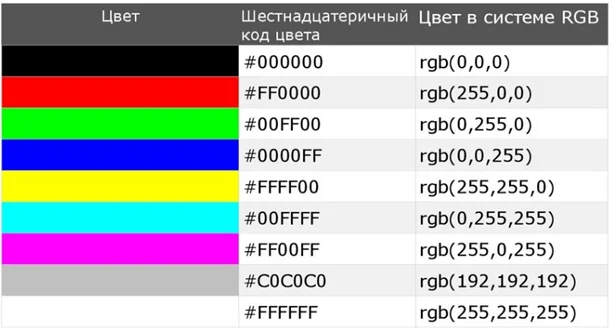
Алгоритм преобразования чисел в 16СС
Способ преобразования аналогичный предыдущим – расписывание числа как многочлена с учетом степеней 16. Для этого число делится на 16, в итоге – перечень остатков от деления, записанных наоборот.
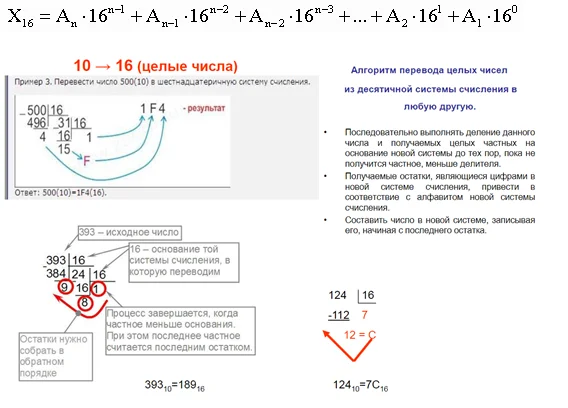
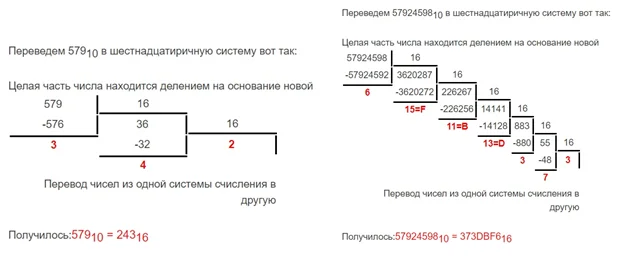
В сети есть калькуляторы, способные выполнять преобразование чисел в различные СС и обратно (некоторые даже с детальным описанием процесса).
Часть 3:
Урок 1. Таблица умножения на 5
1
2
3
4
5
6
7
8
9
10
11
Урок 2. Увеличение (уменьшение) в несколько раз
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 3. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 4. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 5. Таблица умножения на 6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 6. Кратное сравнение
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 7. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 8. Таблица умножения на 7
1
2
3
4
5
6
7
8
9
10
11
12
Урок 9. Окружность
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 10. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 11. Таблица умножения на 8 и на 9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 12. Тысяча
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 13. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 14. Объем фигуры
1
2
3
4
5
6
7
8
9
10
11
12
Урок 15. Умножение и деление на 10 и на 100
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 16. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 17. Свойства умножения
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 18. Умножение круглых чисел
1
2
3
4
5
6
7
8
9
10
11
12
Урок 19. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
Урок 20. Деление круглых чисел
1
2
3
4
5
6
7
8
9
10
Урок 21. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
Урок 22. Умножение суммы на число
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 23. Единицы длины
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 24. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
Урок 25. Деление суммы на число
1
2
3
4
5
6
7
8
Урок 26. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 27. Деление подбором частного
1
2
3
4
5
6
7
8
9
10
11
Урок 28. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
Урок 29. Деление с остатком
1
2
3
4
5
6
7
8
9
10
Урок 30. Деление с остатком
1
2
3
4
5
6
7
8
9
10
11
12
Урок 31. Деление с остатком
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 32. Сети линий. Пути
1
2
3
4
5
6
7
8
Урок 33. Дерево возможностей
1
2
3
4
5
6
7
8
9
10
11
Урок 34. Решение задач
1
2
3
4
5
6
7
8
9
10
Урок 35. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Повторение
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
Часть 3:
Урок 1. Таблица умножения на 5
1
2
3
4
5
6
7
8
9
10
11
Урок 2. Увеличение (уменьшение) в несколько раз
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 3. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 4. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 5. Таблица умножения на 6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 6. Кратное сравнение
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 7. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 8. Таблица умножения на 7
1
2
3
4
5
6
7
8
9
10
11
12
Урок 9. Окружность
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 10. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 11. Таблица умножения на 8 и на 9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 12. Тысяча
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 13. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 14. Объем фигуры
1
2
3
4
5
6
7
8
9
10
11
12
Урок 15. Умножение и деление на 10 и на 100
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 16. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 17. Свойства умножения
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 18. Умножение круглых чисел
1
2
3
4
5
6
7
8
9
10
11
12
Урок 19. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
Урок 20. Деление круглых чисел
1
2
3
4
5
6
7
8
9
10
Урок 21. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
Урок 22. Умножение суммы на число
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 23. Единицы длины
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 24. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
Урок 25. Деление суммы на число
1
2
3
4
5
6
7
8
Урок 26. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 27. Деление подбором частного
1
2
3
4
5
6
7
8
9
10
11
Урок 28. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
Урок 29. Деление с остатком
1
2
3
4
5
6
7
8
9
10
Урок 30. Деление с остатком
1
2
3
4
5
6
7
8
9
10
11
12
Урок 31. Деление с остатком
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 32. Сети линий. Пути
1
2
3
4
5
6
7
8
Урок 33. Дерево возможностей
1
2
3
4
5
6
7
8
9
10
11
Урок 34. Решение задач
1
2
3
4
5
6
7
8
9
10
Урок 35. Решение задач
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Повторение
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109